41
de Poisson como sendo uma fração
da deformação longitudinal e apre-
senta parcelas de deformação elásti-
ca, anelástica e de fluência. Só serão
estudadas aqui as deformação no
concreto provocadas por cargas ex-
ternas. Não serão consideradas as
deformação devidas à variação da
temperatura e retração.
3. A DEFORMAÇÃO ELÁSTICA.
O MÓDULO <<E>>
A relação simples
e
=
E
.
s
estabelecida para
os materiais perfeitamente homogêneos
e isótropos não se verifica em nenhum
dos nossos materiais que apresentam,
em diferentes proporções, tôdas essas
deformações já referidas. Nos concretos
especialmente, as outras deformações im-
pedem sempre a obtenção das medidas
correspondentes às deformações elásti-
cas. Como a inclusão de todo a enorme
gama de influência sob forma de parâme-
tros, iria complicar demais a tão simples
lei de Hooke, têm insistido os pesquisa-
dores em fixar um valor para o “módulo
de elasticidade do concreto”. E assim, é
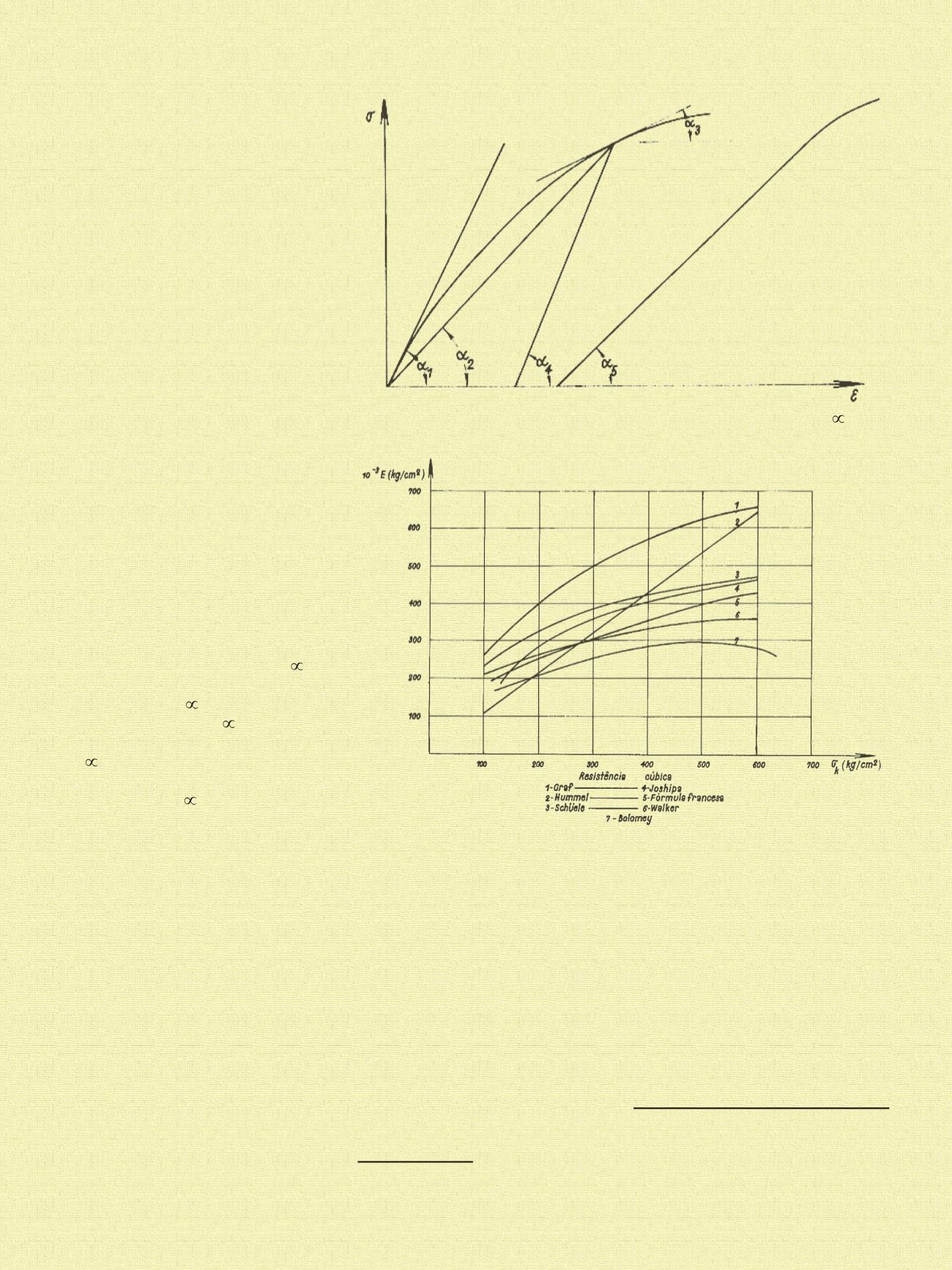
que, enquanto autores (tomando a curva
tensão-deformação) definem “E” como a
inclinação da tangente n origem, ( 1) ou
mesmo na região correspondente à “ten-
são admissível” ( 2), outros preferem a
inclinação da secante ( 3). Outros auto-
res preferem a curva de descarregamento
( 4) à do carregamento e ainda outros
preferem a curva fixada após um carrega-
mento repetido ( 5).
Na Fig. 5 estão as curvas representati-
vas de 4 equações empíricas que rela-
cionam o módulo “E” com a resistência a
compressão do concreto, estabelecidas
em ensaios de compressão simples por
diferentes autores. Tão apenas as dife-
rentes definições utilizadas provocaram
a enorme dispersão que se vê, mas, tam-
bém, as diferentes condições de ensaio,
cura, idade dos concretos e outros fato-
res que tornam difícil qualquer compara-
ção. Se refletirmos que cada uma dessas
curvas está determinada em função de
valôres médios de grande número de
resultados, verificamos o quanto é difícil
uma fixação clara de uma equação para
«E». E essa dispersão se acentua, ainda
mais se a determinação de «E» é feita
através ensaios de compressão e flexão.
Compare-se, p. ex., resultados obtidos
por um mesmo pesquisador — Sachno-
wski em ensaios de compressão simples
e flexão (Fig. 6).
Já em 1930, Glanville estudando o proble-
ma indicava que o procedimento que afas-
taria a participação das deformações não
elásticas, dependentes do tempo, seria
se se pudesse introduzir o carregamento
e medir as deformações em um espaço
de tempo
t
= 0. Com isso era irrealizável,
determinou êle, por extrapolação, através
de resultados de ensaios nos quais o car-
regamento foi introduzido com diferentes
velocidades, uma reta (
t
= 0) que indicava
um comportamento elástico
3
.
3 Para melhores detalhes sobre êsse assunto
seria recomendável a leitura do trabalho
4. A DEFORMAÇÃO
LENTA
A deformação lenta é determinada ge-
ralmente como a soma da fluência com a
deformação anelástica (ou “elástica retar-
dada”). São realmente duas parcelas difí-
ceis de serem medidas em separado. En-
tretanto não devemos esquecer que uma
dessas parcelas —a “ elástica retardada
“ — sendo recuperável, não pode ser de-
signada como deformação plástica.
do Dr. R. Sell, “Der E - Modul des Betons”
realizado no Laboratório de Munique, que
traz além da discussão do problema, uma
sugestão, justificadas em ensaios, para
unificação da definição e determinação
experimental do módulo “E”.
FIG. 4 – DIFERENTES DEFINIÇÕES DO MÓDULO DE ELASTICIDADE DO CONCRETO (E = TG )
FIG. 5 – REPRESENTAÇÃO DE FUNÇÕES PROPOSTAS PARA E = E
s
K
)


