REVISTA ESTRUTURA
| SETEMBRO • 2017
48
Velocidades maiores somente deverão
ser usadas nos casos de fundações iso-
ladas. Entretanto, não se recomendam
valores superiores a V = 5 mm/s.
As referências (1 e 5) mostram vários
gráficos elaborados pela Associação dos
Engenheiros Alemães (VDI), para o controle
de vibrações em fundações de máquinas.
Segundo a VDI, algumas máquinas po-
dem trabalhar sobre suportes com velo-
cidade eficaz (Vef= V/2 ) de até 18 mm /s.
Entretanto, em várias visitas de inspeção
realizadas em instalações industriais, nas
quais constatamos velocidades em torno
de 25 mm s, notamos a impraticabilidade
de qualquer tarefa no local, tornando-se
precária até a instalação dos aparelhos
de medida.
No caso de vibrações horizontais, con-
seguimos recentemente medições com
velocidades em torno de 43 mm/s na fre-
qüência de 200 cpm, resultando · ampli-
tudes de 2 mm.
O leitor por certo pode achar estra-
nho o fato de uma amplitude de tal or-
dem provocar uma resposta insuportá-
vel às pessoas. Entretanto, lembramos
que o desconforto não é função so-
mente da amplitude, mas sobretudo da
direção do movimento e da freqüência
de excitação.
Alguns exemplos mostrados em livros
de Análise Dinâmica não levam em conta
o problema das deformações.
A simples determinação das forças de
restituição com as quais determinamos
os esforços não é suficiente para a solu-
ção do problema dinâmico, o qual exige
deformações adequadas ao conforto hu-
mano e compatíveis com a freqüência de
excitação.
A interação solo-estrutura não pode
ser desprezada, principalmente nos ca-
sos de sistemas com fundações excêntri-
cas e com matriz de massa variável.
Quando o sistema é carregado ex-
centricamente, a fundação experimenta
certa rotação, reduzindo os valores das
frequências naturais, podendo alguma
delas ficar próxima da freqüência de ex-
citação. Em casos assim, a matriz dinâ-
mica é variável e há necessidade da de-
terminação dos limites correspondentes
ao sistema carregado e descarregado.
No caso de a freqüência de excitação fi-
car situada entre os limites, inevitavelmente
o sistema entrará em ressonância quando
carregado ou descarregado, gerando es-
forços cujos valores serão função direta do
amortecimento do sistema e das velocida-
des do carregamento e descarregamento.
Determinada insta lação, em perfei-
to funcionamento em certo local, pode
apresentar problemas com a sua trans-
ferência para outro em que as condições
do solo são diferentes.
A título de ilustração mostraremos u
m exemplo simples em que a fundação
do sistema sofre rotações diferentes em
função das condições do solo, alterando
os valores da matriz de rigidez.
10 – EXEMPLO NUMÉRICO
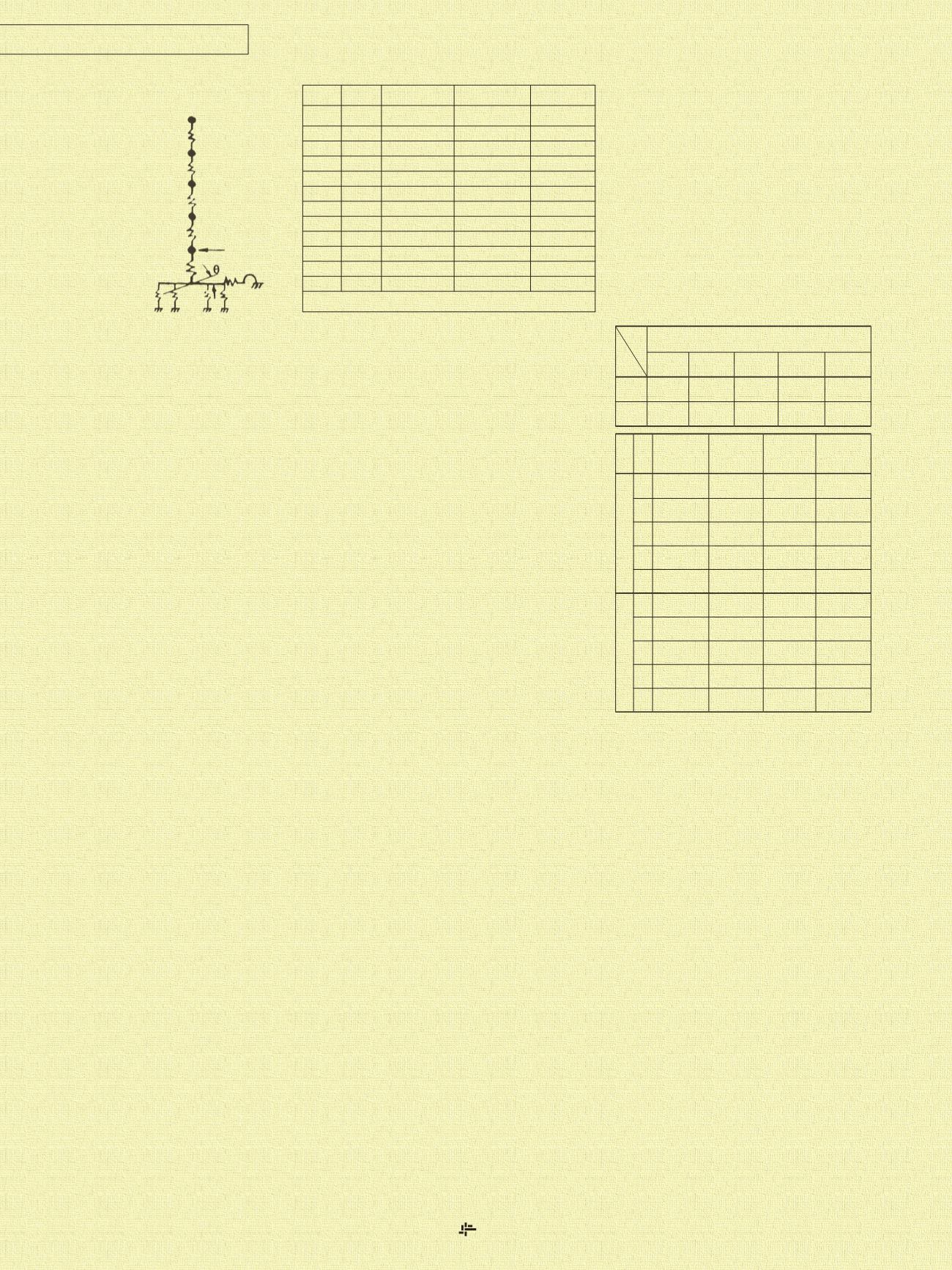
A fig.Nº1 mostra o modelo matemático
para as duas situações criadas pela supo-
sição de solos diferentes, onde nota-se
que as diferenças entre os dois casos são
a rotação (θ) e o índice de amortecimen-
to (c), considerado igual para todos os
modos.
A resolução dos modelos apresentou,
entre outros, os resultados indicados na
Figura 2.
11 – ANÁLISE DOS
RESULTADOS
Como pode ser visto nos quadros da
fig. (2), a rotação maior dada a situação
ω = 23,04 rad/s
f = 3,667 Hz
c
1
= 6%
c
2
= 12%
Θ
1
= 2,8 . 10
-8
Θ
2
= 4,2 . 10
-7
H JT MASSA COORD
I
ts
2
/m m m
2
1 41,38
24,50
(1)
3,80
2 53,42
20,00
(2)
3,80
3 53,42
15,50
(3)
3,80
4 54,70
11,00
(4)
3,80
5 87,54
6,00
(5)
15,20
0,00
E
=
3000000 t/m
2
Fig. 1
22t senω
t
ARTIGO RETRÔ
| REVISTA 47 - 1962
(2) provocou uma redução nas freqüên-
cias naturais da estrutura em relação à
situação (1), resultando na aproximação
da freqüência do 2º modo (4,202 Hz),
da freqüência de excitação (3,667 Hz).
Comparando-se os demais resultados
do aproveitamento puro e simples de um
projeto elaborado para um tipo de solo e
posteriormente colocado em outro.
Usando-se o critério proposto confor-
me a tabela nº1, podemos melhor visuali-
zar o exposto através do quadro da fig. 2.
S
Ne
FREQUÊNCIAS DE VIBRACÃO (Hz)
1º modo 2º modo 3º modo 4º modo 5º modo
(1)
1 ,099 5,826 14,445 27,378 43,850
(2)
0,732 4,202 12,381 26,038 43,363
s JT Aceleração
a (mm/s)
2
Velocidade
V (mm/s)
Amplitude
A (mm)
Restituição
R (t)
(1)
1 -53,197 -2,308 -0,100 -2,205
2 -8,962 -0,389 -0,016 -0,482
3 25,573 1,109 0,048 1,343
4 40,297 1,749 0,075 2,176
5 27,483 1,192 0,051 24,379
(2)
1 -257,374 -11,170 -0,484 -9,780
2 - 47,150 -2,046 -0,088 -2,439
3 119,847 5,201 0,225 5 ,590
4 197,445 8,569 0,371 9,617
5 149,292 6,479 0,281 33,734
Fig. 2
12 – PRINCIPAIS
REFERENCIAS
BIBLIOGRÁFICAS
1. Buzdugan, G. - Dynamique Des Foun-
dations de Machines - Editions Eyrolles
- Paris - 1972
2. Crandell, F.J. - Ground Vibration Due To
Blasting And lts Effect Upon Structures
- J. Boston Soc. Civil Engrs., 36 num2 -
1949
3. Hendron, Jr., A. J. - Structural And Geo-
technical Mechanics Prentice - Hall, lnc.
- 1977
4. Hendron, Jr., A. J. - Stagg-Zienkiewicz -
Rock Mechanics In Engineering Pratice
John Wiley Sons - London - 1968
5. Major Alexander - Dynamics in Civil En-
gineering - Akademiai Kiadó - Budapest
- 1980
6. Pereira Lopes, Mauro - Estabilidade
das Construções de Grande Altura -
Estrutura nº 86 - 1979


