35
Com base nos resultados dos ensaios
dos corpos de prova extraídos (ou seja,
na determinação da resistência à com-
pressão axial) e dos respectivos resulta-
dos dos índices esclerométricos (deter-
minação das suas durezas superficiais)
nos mesmos elementos estruturais e
locais onde se executarão as devidas ex-
trações de testemunhos, determina-se a
curva de correlação linear entre os valo-
res dos dois resultados de ensaios dis-
tintos destes concretos ensaiados para
uma determinada obra executada em
qualquer período ou data. A expressão
que relaciona a resistência à compres-
são com a dureza superficial do con-
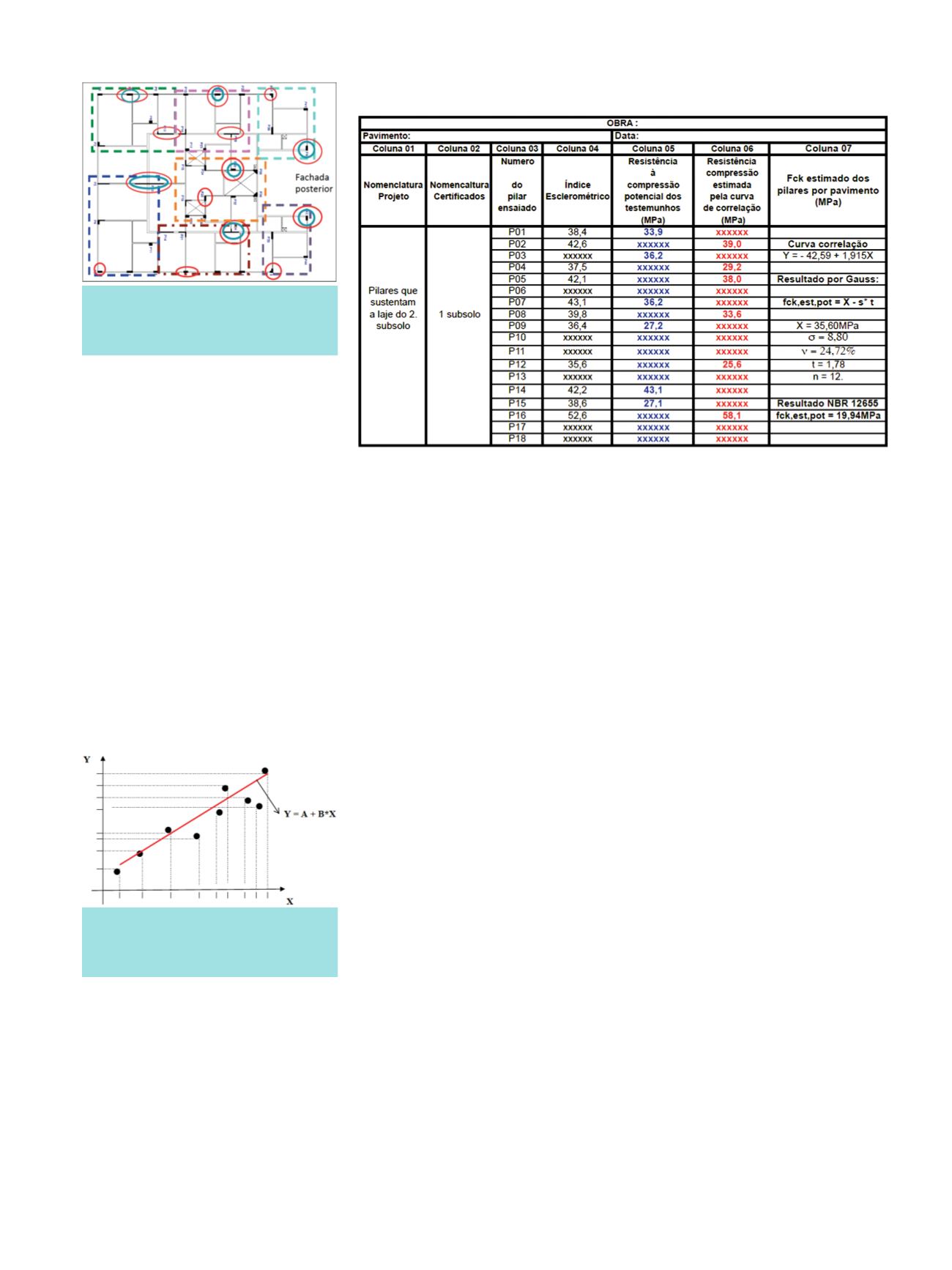
creto é a regressão linear de uma reta,
como segue a
figura 5
e representada
pela equação que segue:
Y = A + B * X
, onde:
Y
= Valor da resistência característi-
ca mecânica estimada (ensaio me-
cânico);
X
= Valor do índice esclerométrico
obtido no ensaio (ensaio físico);
A
= Constante calculada;
B
= Constante calculada.
Esta equação representa a reta média
entre a interpolação dos resultados em
um gráfico X e Y, onde X representa todos
os valores obtidos nos ensaios de dureza
superficial e Y, os valores obtidos nos en-
saios de ruptura à compressão axial dos
testemunhos extraídos e rompidos na
prensa hidráulica.
Com esta equação, estimam-se valores
de resistência mecânica à compressão
em pilares onde somente foram procedi-
dos ensaios esclerométricos, pois enten-
de-se que a concretagem dos pavimentos
foi executada com concreto distintos em
datas diferentes. A
tabela 1
indica exem-
plos de valores hipotéticos, onde em azul
são os valores obtidos das resistências
estimadas dos pilares com base na equa-
ção de correlação, onde foram somente
executados os ensaios de esclerometria
e a equação da curva de correlação linear
do pavimento analisado; e em vermelho
são os valores de
f
ck,pot,est
obtidos da cor-
relação linear entre o índice e o
f
ck,pot,ext
.
Aceitação do concreto e obtenção do
f
ck,pot,est
pode ser obtido por dois meios,
como indicado na tabela 1, sendo eles:
a) Distribuição normal denominada
como Gauss: A distribuição nor-
mal ou de Gauss é um modelo
matemático que pode represen-
tar de maneira satisfatória a dis-
tribuição das resistências à com-
pressão do concreto sempre que
o coeficiente de variação (
v
c
%)
observado seja igual ou menor a
30% (Vieira, 2007, p. 68).
b) Determinação da resistência pela
ABNT NBR 12655:2015: Esta norma
considera dois tipos de controle de
resistência: o controle estatístico do
concreto por amostragem parcial e
o controle do concreto por amos-
tragem total. Para o controle por
amostragem parcial é prevista uma
forma de cálculo do valor estimado
da resistência característica (
f
ck,pot,
est
) do lote de concreto em estudo.
Obs.: As quantidades de corpos de
prova e ensaios do índice de dureza
superficial poderão ser aumenta-
das, conforme forem se obtendo os
resultados de ruptura dos testemu-
nhos do laboratório, ou seja, se os
resultados forem não conformes,
se faz necessária a extração de
mais corpos de prova, com o aval
do projetista estrutural, dos pilares
mais solicitados.
5.2 – Considerações
quanto aos aspectos de
segurança na estrutura:
Os resultados
f
ck,pot,est
obtidos dos con-
cretos extraídos de uma estrutura são
muito mais representativos do que os
resultados obtidos dos corpos de prova
moldados e rompidos que representam
o concreto lançado em uma estrutura,
que podem, durante as moldagens, so-
frer falhas ao não serem exatamente
os que potencialmente foram lançados,
adensados e curados na estrutura em
condições que não são 100% de pleno
FIGURA 4 – PLANTA DA ESTRUTURA DOS
PILARES ONDE SERÃO EXECUTADOS
ENSAIOS ESCLEROMÉTRICOS E EXTRAÇÃO
DE TESTEMUNHOS
FIGURA 5 – ILUSTRAÇÃO ESQUEMÁTICA DA
CURVA DE CORRELAÇÃO LINEAR
FONTE: GRÁFICO ELABORADO PELO AUTOR
(TOMAZELI, 2015, P. 38)
TABELA 1 –
REPRESENTAÇÃO FINAL DAS RESISTÊNCIAS ESTIMADAS COM BASE NA CURVA DE
CORRELAÇÃO DO LOTE DE CONCRETO ANALISADO


